Squarefree word

In combinatorics, a square-free word is a word that does not contain any subword twice in a row. There exist infinite square-free words in any alphabet with three or more symbols, as proved by Axel Thue^[1] ^[2]. To build an infinite square-free word in the alphabet {a, b, c}, let 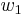$w_1$ be any word starting with the letter a. Define the words 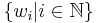$\{w_{i} | i \in \mathbb{N} \}$ recursively as follows: the word 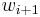$w_{i%2B1}$ is obtained from 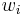$w_{i}$ by replacing each a in 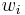$w_i$ with abcbacbcabcba, each b with bcacbacabcacb, and each c with cabacbabcabac (this example was found by J. Leech ^[3]). It is possible to check that the sequence converges to the infinite square-free word abcbacbcabcbabcacbacabcacbcabacbabcabacbcacbacabcacb...

Over a two-letter alphabet {a, b} the only square-free words are the empty word and a, b, ab, ba, aba, and bab. There is, however, an infinite cube-free word: the Thue-Morse sequence.

The Thue number of a graph G is the smallest number k such that G has a k-coloring for which the sequence of colors along every non-repeating path is squarefree.

Notes

^ A. Thue, Über unendliche Zeichenreihen, Norske Vid. Skrifter I Mat.- Nat. Kl., Christiania 7 (1906) 1–22.
^ A. Thue, Über die gegenseitige Lage gleicher Teile gewisser Zeichenreihen, Norske Vid. Skrifter I Mat.-Nat. Kl., Christiania 1 (1912) 1–67.
^ J. Leech, A problem on strings of beads, Math. Gazette 41 (1957) 277– 278.

References

Lothaire, M. (1997), Combinatorics on words, Cambridge: Cambridge University Press, ISBN 0-521-59924-5 .